About Castro

Castro at a glance
1-, 2-, and 3-dimensional unsplit, 2nd-order hydrodynamics
multigroup flux-limited diffusion radiation hydrodynamics
constrained transport corner-transport upwind ideal MHD (single level only currently)
adaptive mesh refinement with subcycling; jumps of 2x and 4x between levels
arbitrary equation of state (gamma-law and stellar EOSes are bundled)
general nuclear reaction networks
Strang split or spectral deferred corrections time integration
explicit thermal diffusion
full Poisson gravity (with isolated boundary conditions)
Rotation (in the co-rotating frame) in 2-d axisymmetric and 3-d.
parallelization via MPI + OpenMP (CPUs), MPI + CUDA (NVIDIA GPUs), or MPI + HIP (AMD GPUs)

Documentation
The code structure and algorithm are described in the Castro User's Guide

hydrodynamics + gravity

Castro's hydrodynamics is based on a compressible flow formulation in Eulerian coordinates. Castro uses a dimensionally-unsplit 2nd order Godunov method for construct the fluxes through the interfaces of each cell (a choice of piecewise linear or piecewise parabolic reconstruction + characteristic tracing is provided). The hydrodynamics is designed to work with a general (convex) equation of state, and a variety of Riemann solvers are provided.

Newtonian gravitational forces are supported through either a simple monopole approximation or the full Poisson equation using geometry multigrid. Isolated boundary conditions for the Poisson solver allow for modeling complex mass distributions. Several implementations for incorporating gravity into the energy equation are implemented, including an explicit source term and a conservative flux formulation.

adaptive mesh refinement

Castro uses the AMReX library for adaptive mesh refinement (AMR). Our approach uses a nested hierarchy of logically-rectangular grids with simultaneous refinement of the grids in both space and time. The integration algorithm on the grid hierarchy is a recursive procedure in which coarse grids are advanced in time, fine grids are advanced multiple steps to reach the same time as the coarse grids and the data at different levels are then synchronized. A separate synchronization is done for gravity.

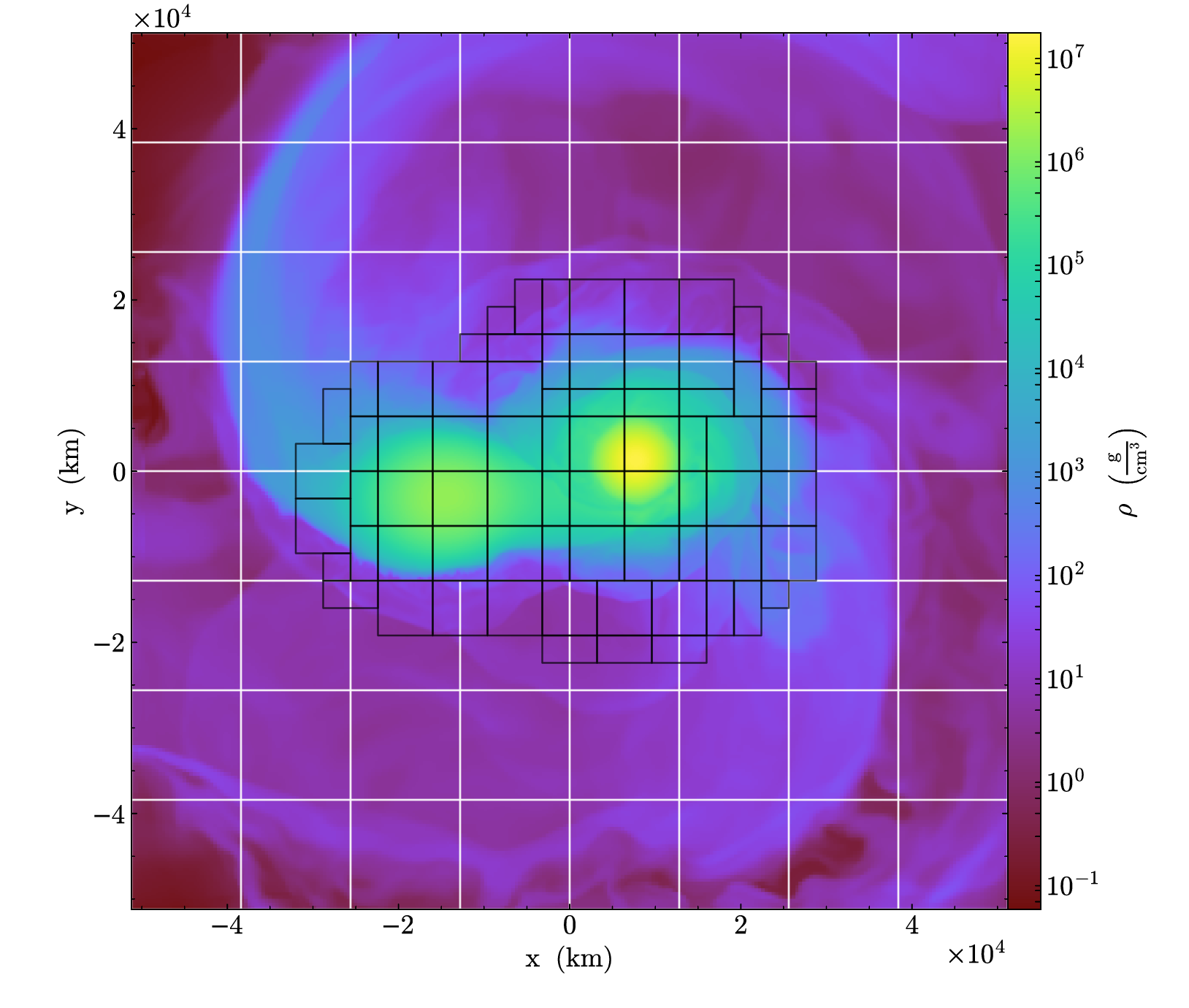
AMReX grid showing 2 levels.

radiation

Radiation support includes gray or multigroup flux limited diffusion in a mixed-frame or comoving frame, including all coupling terms to O(v/c). The radiation update is done implicitly using the linear solvers provided by the hypre package.

MHD

Ideal MHD is supported through a constrained transport, unsplit (corner transport upwind) solver. This works together with our general equation of state and reaction networks, all the source terms, and the simplified spectral deferred corrections time integration code path.

equations of state, reaction networks, and other microphysics

A wide variety of equations of state, reaction networks, conductivities, and other physics inputs are provided by the Microphysics git repo. Maintaining them in a separate repo allows all of the AMReX astrophysics codes share the same microphysics. A new reaction network can easily be created using the pynucastro library, which will directly output the C++ code needed by Castro/Microphysics with all of the rates and network links.

time-integration

The default solver use a second-order accurate update of hydrodynamics with Strang splitting to couple the reaction sources. Two different time-integration techniques are available: the simplified spectral deferred corrections (SDC) method uses the same hydrodynamics reconstruction but solves the coupled hydro-reaction system using the full stiff reaction integration and a piecewise-constant-in-time hydrodynamics source. The true SDC method uses solves a nonlinear update for the coupled evolution of the reacting hydro system with either a 2nd order or 4th order (in space and time) discretization. Both of these methods strongly couple reactions and hydro, which is important for explosive astrophysical flows.

reproducibility

All Castro plotfiles store information about the build environment (build machine, build date, compiler version and flags), run environment (output date, output dir, number of processors, wall clock time), and code versions used (git hashes for the main Castro source and AMReX source, and support repos, if available). This allows for a recovery of the code base used for previous results.

Castro is run through a nightly regression test suite that checks the output, bit-for-bit, against stored benchmarks for many of the problem setups (including real science runs).

parallel performance

Castro uses a hybrid programming model based on MPI and OpenMP. Distribution of grid patches to nodes using MPI provides a natural coarse-grained approach to distributing the computational work, while threading of loops over zones in a grid using OpenMP provides effective fine-grained parallelization. Castro uses a new tiled approach to OpenMP that can effectively take advantage of manycore processors like the Intel Phi's.

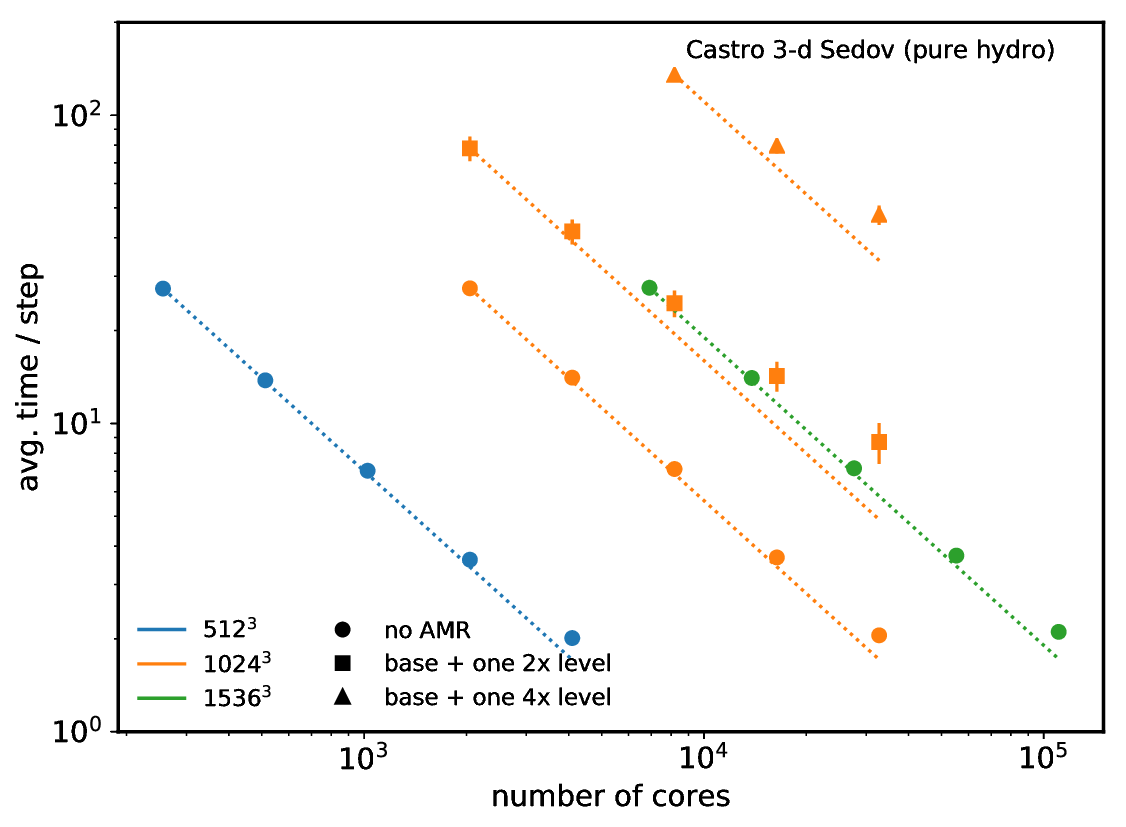
Castro strong scaling for a pure hydro + real EOS Sedov problem on the OLCF titan machine.

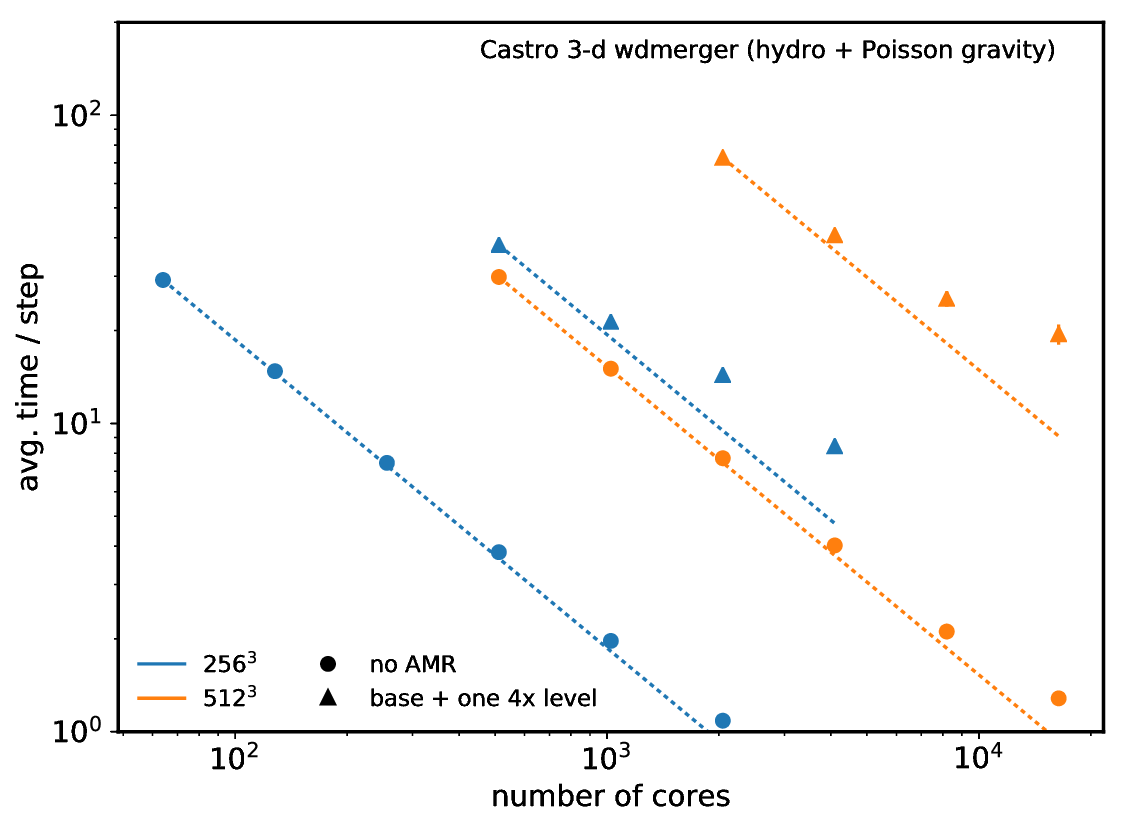
Castro strong scaling for the WD merger problem with full Poisson gravity on the OLCF titan machine.

GPU performance

Castro offloads to GPUs using using the same computational kernels as we do with MPI+OpenMP. All of the solvers (aside from the true-SDC) run fully on GPUs, allowing us to run entire simulations on GPUs. Castro has run with both NVIDIA and AMD GPUs.

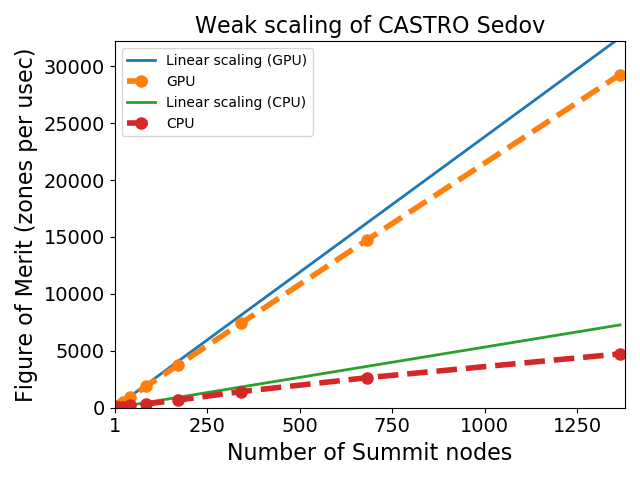
GPU weak scaling on Summit for the Sedov problem. We see that the GPU version (6 GPUs /node) of the problem is about an order of magnitude faster than the CPU version (6 MPI × 7 OpenMP threads per MPI on each node).

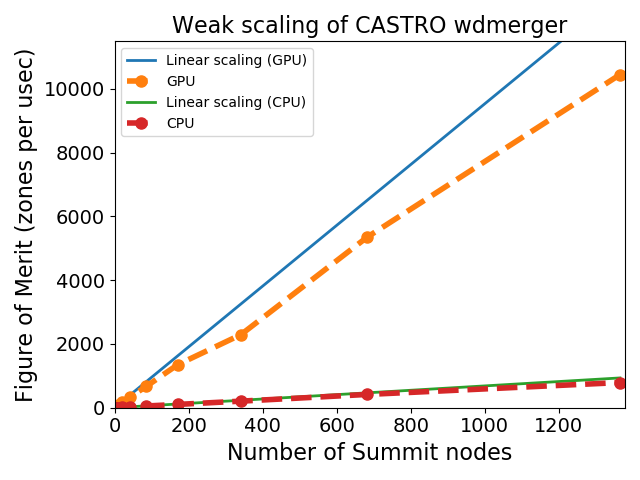
GPU weak scaling on Summit for the WD merger problem. We see that the GPU version (6 GPUs /node) of the problem is much faster than the CPU version (6 MPI × 7 OpenMP threads per MPI on each node).

Castro at a glance

Documentation