ODE Integrators

Available integrators

We use a high-order implicit ODE solver for integrating the reaction system. A few alternatives, including first order implicit and explicit integrators are also provided. Internally, the integrators use different data structures to store the integration progress, and each integrator needs to provide a routine to convert from the integrator’s internal representation to the burn_t type required by the actual_rhs and actual_jac routine.

The name of the integrator can be selected at compile time using the INTEGRATOR_DIR variable in the makefile. Presently, the allowed options are:

  • BackwardEuler: an implicit first-order accurate backward-Euler method. An error estimate is done by taking 2 half steps and comparing to a single full step. This error is then used to control the timestep by using the local truncation error scaling.

  • ForwardEuler: an explicit first-order forward-Euler method. This is meant for testing purposes only. No Jacobian is needed.

  • QSS: the quasi-steady-state method of [MOvanLeer00] (see also [GH13]). This uses a second-order predictor-corrector method, and is designed specifically for handling coupled ODE systems for chemical and nuclear reactions. However, this integrator has difficulty near NSE, so we don’t recommend its use in production for nuclear astrophysics.

  • RKC: a stabilized explicit Runge-Kutta-Chebyshev integrator based on [SSV98]. This does not require a Jacobian, but does need to estimate the spectral radius of the system, which is done internally. This works for moderately stiff problems.

    The spectral radius is estimated by default using the power method, built into RKC. Alternately, by setting integrator.use_circle_theorem=1, the Gershgorin circle theorem is used instead.

  • VODE: the VODE [BBH89] integration package. We ported this integrator to C++ and removed the non-stiff integration code paths.

    Note

    The VODE integrator uses Jacobian caching when run on a CPU by default. This can be disabled at runtime by setting integrator.use_jacobian_caching = 0.

    On GPUs, we disable Jacobian caching due to the increased memory needs. Jacobian caching on GPUs can be enabled by explicitly setting the build parameter USE_JACOBIAN_CACHING=TRUE.

We recommend that you use the VODE solver, as it is the most robust.

Note

The runtime parameter integrator.scale_system will scale the internal energy that the integrator sees by the initial value of \(e\) to make the system \(\mathcal{O}(1)\). The value of atol_enuc will likewise be scaled. This works for both Strang and simplified-SDC. For the RKC integrator, this is enabled by default.

For most integrators this algebraic change should not affect the output to more than roundoff, but the option is included to allow for some different integration approaches in the future.

This option currently does not work with the ForwardEuler or QSS integrators.

Timestep selection

All of the integrators will select the timestep internally to meet the tolerances. There are 2 controls that affect timestepping:

  • integrator.ode_max_dt : sets the maximum allowed timestep

  • integrator.ode_max_steps : sets the maximum number of steps the integrator is allowed to take. If it exceeds this, then it will return an error.

Linear algebra

All implicit integrators use the LINPACK LU decomposition routines.

For the templated networks (aprox13, aprox19, …) the implementation is done using consexpr loops over the equations and no pivoting is allowed.

For the other networks (usually pynucastro networks), the implementation is provided in Microphysics/util/linpack.H and is templated on the number of equations. Pivoting can be disabled by setting integrator.linalg_do_pivoting=0.

Integration errors

Important

The integrator will not abort if it encounters trouble. Instead it will set burn_t burn_state.success = false on exit. It is up to the application code to handle the failure.

The burn_t error_code field will provide an error code that can be used to interpret the failure. The current codes are:

code

meaning

1

success

-1

invalid inputs

-2

underflow in computing \(\Delta t\)

-3

spectral radius estimation did not converge

-4

too many steps needed

-5

unable to meet the accuracy demanded by the tolerances

-6

non-convergence in the corrector iteration

-7

LU decomposition failed

-100

entered NSE

Tolerances

Tolerances dictate how accurate the ODE solver must be while solving equations during a simulation. Typically, the smaller the tolerance is, the more accurate the results will be. However, if the tolerance is too small, the code may run for too long or the ODE solver will never converge. In these simulations, rtol values will set the relative tolerances and atol values will set the absolute tolerances for the ODE solver. Often, one can find and set these values in an input file for a simulation.

Fig. 1 shows the results of a simple simulation using the burn_cell unit test to determine what tolerances are ideal for simulations. For this investigation, it was assumed that a run with a tolerance of \(10^{-12}\) corresponded to an exact result, so it is used as the basis for the rest of the tests. From the figure, one can infer that the \(10^{-3}\) and \(10^{-6}\) tolerances do not yield the most accurate results because their relative error values are fairly large. However, the test with a tolerance of \(10^{-9}\) is accurate and not so low that it takes incredible amounts of computer time, so \(10^{-9}\) should be used as the default tolerance in future simulations.

Relative error plot

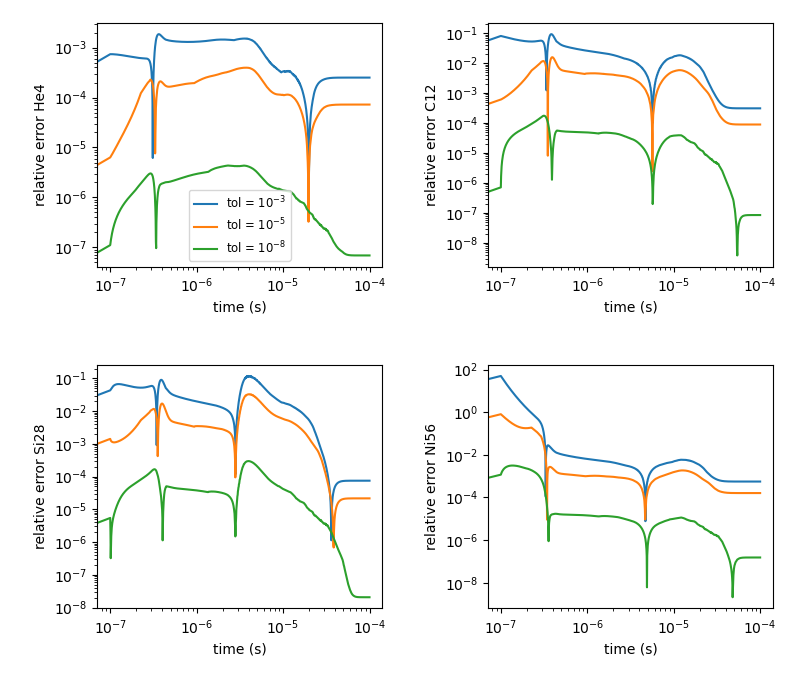
Fig. 1 Relative error of runs with varying tolerances as compared to a run with an ODE tolerance of \(10^{-12}\).

The integration tolerances for the burn are controlled by rtol_spec and rtol_enuc, which are the relative error tolerances for (1) and (2), respectively. There are corresponding atol parameters for the absolute error tolerances. Note that not all integrators handle error tolerances the same way—see the sections below for integrator-specific information.

The absolute error tolerances are set by default to \(10^{-12}\) for the species, and a relative tolerance of \(10^{-6}\) is used for the temperature and energy.

Controlling Species \(\sum_k X_k = 1\)

The ODE integrators don’t know about the constraint that

\[\sum_k X_k = 1\]

so this is only going to be preserved to the level that the integrator tolerances allow. There are a few parameters that help enforce this constraint on the intermediate states during the integration.

  • integrator.renormalize_abundances : this controls whether we renormalize the abundances so that the mass fractions sum to one during a burn.

    This has the positive benefit that in some cases it can prevent the integrator from going off to infinity or otherwise go crazy; a possible negative benefit is that it may slow down convergence because it interferes with the integration scheme. Regardless of whether you enable this, we will always ensure that the mass fractions stay positive and larger than some floor small_x.

    This option is disabled by default.

  • integrator.SMALL_X_SAFE : this is the floor on the mass fractions. The default is 1.e-30.

  • integrator.do_species_clip : this enforces that the mass fractions all in \([\mathtt{SMALL\_X\_SAFE}, 1.0]\).

    This is enabled by default.

Retry Mechanism

Integration can fail for a number of reasons. Some of the errors you may see are:

  1. Not enough steps allowed (integrator.ode_max_steps)

  2. The timestep selected by the integrator is too small (comparable to roundoff)

  3. The final abundances do not sum to 1.

There can be a number of reasons for these failures, including:

  • The Jacobian is not accurate enough

    This can lead to issues 1 or 2 above

  • The integrator is not appropriate for the thermodynamic conditions

    For example, the RKC integrator may be working too hard, leading to issue 1.

  • The tolerances you are requesting are too tight

    This can lead to issues 1 or 2 above

  • The tolerances (in particular, integrator.atol_spec) are too loose

    This can lead to issue 3 above

  • The evolution is entering NSE

    This can lead to issue 1.

The integrator() function that calls the actual integrator drive for the choice of integrator allows for a retry if a burn failure was detected. This is enabled by setting

integrator.use_burn_retry = 1

This will call the same integrator again, restarting from the initial conditions but with a different choice of tolerances and Jacobian. The runtime parameters that come into play when doing the retry are:

  • retry_swap_jacobian : do we swap that Jacobian type for the retry (i.e. use the numerical Jacobian if we try the analytic Jacobian for the first attempt)

  • retry_rtol_spec : relative tolerance for the species on retry

  • retry_rtol_enuc : relative tolerance for the energy on retry

  • retry_atol_spec : absolute tolerance for the species on retry

  • retry_atol_enuc : absolute tolerance for the energy on retry

Note

If you set any of the retry tolerances to be less than \(0\), then the original (non-retry) tolerance is used on retry. The default value for all of the retry tolerances is \(-1\), which means the same tolerances are used on retry unless you override them at runtime.

Tip

Sometimes a simulation runs best if you set integrator.ode_max_steps to a small value (like 10000) and start with the analytic Jacobian (integrator.jacobian = 1) and then use the retry mechanism to swap the Jacobian on any zones that fail.